当前位置: 主页 > 论文下载 > 教育论文 >

让课堂充满问题让问题充满思考

作者：殷海霞日期：2013-12-03 09:36 来源：《语数外学习》数学教育

（丹阳市吕城初级中学，江苏镇江 212351）

摘  要：问题是数学的心脏，构建恰时恰点的问题是有效教学的基本线索，“问题引导学习”应当成为我们的一种追求。然而，反思我们的数学课堂，许多教师将提问看作是一种很简单的教学方式，没有深入地思考运用时应遵循的一系列原则、技能和技巧；问题缺乏针对性和推进性，质量不高，缺乏艺术性，单调。在课堂教学中，如何把探究性学习方式用好用活呢？我们的体会是：让课堂充满问题，让问题充满思考。
关键词：问题；课堂；思考
中图分类号：G633    文献标识码：A        文章编号：

一、关注教材知识的重难点
教材的重点难点是教学的重心所在，是学生认知矛盾的焦点，也是数学教学的基本特征之一。学生往往学有困难，很难引起主动探索的积极性。
例如，在学习函数的概念时，我围绕函数概念设计以下问题：
问题1：函数有几个变量，它是一种怎样的对应关系？
问题2：函数y=2x中如何求自变量x=-1时y的值？
问题3：自变量是否一定要用x表示？对于函数y=和圆面积S=πr2,自变量x，r是否可以取任何值？它们的取值范围应考虑什么
问题4：下列各式能表示y是x的函数吗？为什么？
A、y=2x-1    B、y=2     C、y=x2     D、y=±x
“导向明确、有的放矢“的问题设计，着眼于学生的可持续发展，使学生体会知识的发生过程，理解问题的根本特征。
二、关注学生思维的障碍点
数学知识不仅靠—些既得知识而构成，还要靠思维链建立起有血有肉的生机勃勃的知识方法体系。

“拓思破障，深入本质”的问题设计，着眼于学生思维的发展，帮助学生透析问题实质，引导学生去思考去领悟，并把这种领悟扩展整个数学空间。
三、关注教学内容的深化点
课堂教学中教师有效的引导学生以现有的新知识去吸纳同化新的知识，用新的经验和要求去修正和顺应原有的认知结构，能达到既深化知识，又发展能力的目的。

（1）BC为直径可想到所对的圆周角为直角，联想直角三角形的知识。
（2）Q为AC中点，可联想三角形中位线和直角三角形斜边中线性质。
（3）要证PQ为切线，可联想到“连半径，证垂直”
从一题多解去发展学生的思维能力，能拓展学生的知识面，但仅仅在这一层面还不够，我继续深入提问:
问题1：把点Q为AC中点与结论“PQ为⊙O的切线”互换。你能证明吗？
问题2：把点Q为AC中点，换成OQ∥AB。你还有什么结论？
问题3：给一定的数据，你能计算解答吗？如BC=2，∠A=30°，你能得到那些答案。
这样的问题可以使学生明白通常有许多途径去解剖一道题，使学生明白解题不仅仅是得到答案，而是发现数学的关联和思想。
“横纵联系、拓展延伸”的问题设计，既给学生以充分自由选择的空间，引发学生参与讨论。同时让学生经过深入思考，自主理解、感悟，训练的是思维、提升的是能力。
四、关注知识网络的整合点
数学知识之间存在密不可分的联系，最佳知识结构是一张知识网络，在知识网络的整合处设计问题，使得知识互相渗透，互相组合。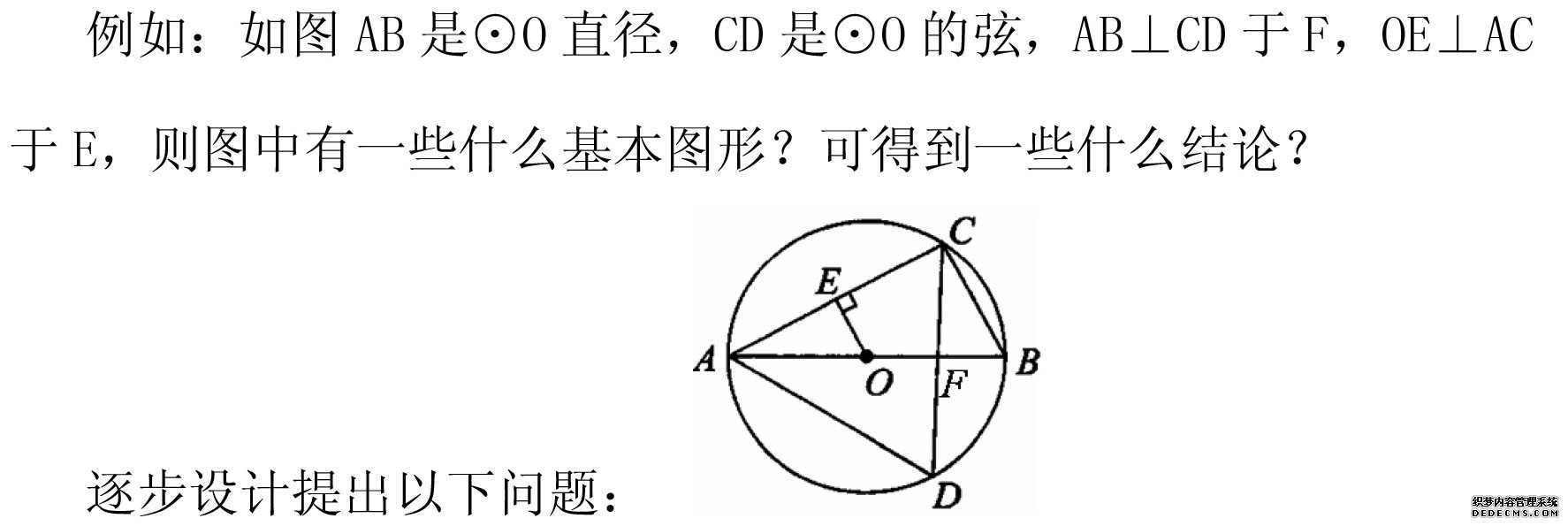

问题1：有些什么线段？用与圆知识有关的概念表达。
问题2：有些什么角？用与圆知识有关的概念表达。
问题3：有些什么三角形？为什么？
问题4：若AB⊥CD于F，OE＝OF，图中有哪些线段、角、弧相等？为什么？
问题5：请你假设已知图中的二条线段为已知，尝试能否求得其他所有线段的长度？
这样的问题设计所涉及的知识有图形、概念、图形之间的关系、知识块之间的联系、对知识的检索、对规律的认识，有直觉和知识的联系，有记忆和理解的联系，有感悟和推理的联系，有规则和定理的联系，有表达和逻辑的联系。
“以点带面、结构优化”的问题设计，使得整个问题系统围绕着知识、能力结构的核心目标展开。学生积极进入思维状态，促进学生为解决问题而对相关知识进行检索，将它们从零碎的，无组织和无序的状态中提取出来，重新加以组织，形成一个有用的网络。
总之，我们在新的教学改革实践中要做到以发现问题为主导，用问题联系生活实际，可以提高学生的学习趣味性，使课堂充满思考，进而培养出有创造意识、创新精神和较强解决实际问题能力的学生。让我们在新的工作中更新观念，努力探究教学中的问题设置，加强学法指导，关注学生的内心世界，发挥学生的潜能，突出学生的自主地位，使“以人为本”的教学理念得到真正的落实。