| 【文章摘要】 烟气含氧量是评价火电厂锅炉燃烧好坏的一项重要指标,所以准确的测量尤为重要。本文主要研究内容是利用软测量技术对电厂烟气含氧量进行仿真测量,所采用的软测量建模方法为数据成组处理法 (Group method of data handling, GMDH),利用从华润某电厂300MW机组得到的实际运行数据建立模型,并与BP神经网络所得预测结果进行对比。仿真结果表明:该方法能够较准确的对火电厂烟气含氧量进行预测。 【关键词】 烟气含氧量 ;软测量 ;GMDH 0 引言 火电厂作为我国电力发展的主力军,其发电量仍在我国总发电量中占有很高的份额。电厂的经济运行与锅炉燃烧效率的高低有直接关系,判断锅炉燃烧效率的方法,一般是通过过剩空气系数来确定的,但是直接测量过剩空气系数目前比较困难,一般来说是通过测量与过剩空气系数密切相关的烟气中氧气的含量来间接确定。 软测量技术主要由辅助变量的选择、数据采集和处理、软测量模型及在线校正四个部分组成,而建模方法的选择是重点。 本文所采用的建模方法为数据成组处理法,它是一种以多层神经网络原理和自组织结构思想为指导,适用于复杂非线性系统的启发式自组织建模方法。由前苏联学者A. G. Ivaknenko在60年代末提出。该方法对于复杂系统的建模、预测表现出良好的效果,因此很快就受到了各国学者的重视,并对其进行了许多改进和发展研究。此方法在烟气含氧量的软测量方面目前还没有应用。 1 辅助变量的选取及数据预处理 a) 辅助变量的选取 本文所采用的辅助变量选取方法是:先计算出各个变量与烟气含氧量的相关系数,再用主元分析法确定主元的个数k。 一般情况下,选择累积贡献率超过85%的k个主元。经分析前8个主元的累积贡献率达到了88.311%,则可确定主元个数为8 个。 b) 数据预处理 数据中的误差分为随机误差和过失误差,本文采用滑动平均法对数据进行平滑处理,去除了随机误差。再用Grubbs检验法来检验过失误差,确定数据中的误差后将其剔除,得到适合建模的数据。 2 GMDH 建模 c) GMDH 算法的基本原理 对于一个未知的非线性系统,GMDH算法常用高阶 Kolmorgorov-Gaber 多项式(式(1))来描述。经过多层筛选,利用局部简单的参考函数不断逼近式(1),从而得到足够复杂的模型。 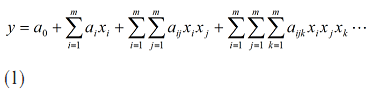 GMDH算法所采用的数据结构与多元回归模型相类似。通常将所获得的数据分成两个子集:训练集和检验集。这么做的目的是为了对模型进行交叉验证以防止过拟合,使模型保持正则化。传统的GMDH网络利用如下所示的式子建立每一层的输入输出关系,用以进行逐次逼近得到最终模型 : 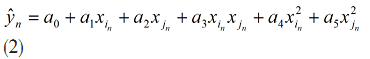 其中 为系数, 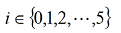 ,上式为二次项形式的参考方程,当然也可根据系统的复杂程度选择更复杂的形式。 ,上式为二次项形式的参考方程,当然也可根据系统的复杂程度选择更复杂的形式。d) GMDH 算法建模步骤 (1)将用于建模的数据分成两组:训练组和测试组。 (2)根据式(2),利用训练组数据计算每一对输入数据  的参考方程参数和相应的输出 ,所有数输入数据对计算得出的输出构成第一层的中间变量 ; 的参考方程参数和相应的输出 ,所有数输入数据对计算得出的输出构成第一层的中间变量 ;(3)在测试集上利用式(3)计算第一层的中间变量的准则值e 。选取一个阈值,若中间变量的准则值e<R ,则保留该变量。所有变量都经过筛选之后,将保留的变量作为新的输入计算出下一层的变量; (4)记录每层变量所得最小准则值emin,当网络训练到第k层时,若 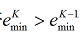 ,则训练停止,第K-1层得到最小准则值的方程为最终最优方程。将方程中的各项回溯至最初始变量,即用来 ,则训练停止,第K-1层得到最小准则值的方程为最终最优方程。将方程中的各项回溯至最初始变量,即用来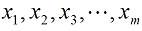 表示最终方程。 表示最终方程。3 仿真实验结果 建模所用数据总数为500个,将分成两组,其中前400个数据归入训练组,后100个数据归入测试组,分别导入GMDH网络和BP神经网络进行建模。BP神经网络的学习因子设置为 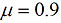 ,学习速率目 标误差为 ,学习速率目 标误差为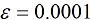 。 。对比两种方法所得结果的均方根误差(RMSE),平均绝对误差(MAE)以及最大正负误差,如表 1 所示。可见,GMDH 预测结果的各项误差均优于BP神经网络,说明 GMDH 网络建模效果很好。表1 GMDH网络和BP神经网络误差对比  4 结论 本文所采用的GMDH网络,在软测量建模中目前应用的还比较少,利用电厂实际运行数据对烟气含氧量进行建模预测,所得的结果与应用较多的BP神经网络相比误差更小,预测精度更高,在软测量建模中有很大的应用潜力。 【参考文献】 [1]陈敏.火电厂锅炉烟气含氧量预测及燃烧系统优化研究[硕士学位论文 ]. 北京 :北京交通大学,2011 [2]俞金寿. 软测量技术及其应用[J].自动化仪表,2008,29(1):1~7 [3]Dong-hyuk L,Sung-han L, Man-gyun N.Smart Soft-sensing for Feedwater Flowrate at PWRs Using a GMDH Algorithm[C].IEEE Transactions on Nuclear Science,2010,57(1): 340~347 |