当前位置: 主页 > 论文下载 > 计算机论文 >

LDPC码编译码原理概述

作者：杨柳日期：2015-11-04 10:53 来源：未知

一、LDPC 码概述
LDPC码是一种低密度奇偶校验码。LDPC码的译码比较简单，具有逼近香农极限的特点。LDPC码是一种线性分组码的一种，其校验矩阵中非零元素的个数是很少的。由于校验矩阵 H 的这种稀疏性，从而保证了译码复杂度和最小码距都只随码长的增大而呈线性增加的趋势。
二、LDPC 码的基本构造方法
2.1 MacKay 和 Neal 构造的规则随机 LDPC 码LDPC码的这种构造方法，是通过检查其校验矩阵H的任意两列，同一位置是否都为1，通过这种方法可以避免最短四环的出现。对于码长比较大的LDPC码，其校验矩阵会非常稀疏，出现最短4环的可能性会非常小。在LDPC码的码长较短的情况下，也可以构造出无 4 环的校验矩阵。MacKay和Neal所提出的构造方法，应用到实际当中是很难的，是由于它的校验矩阵和生成矩阵不具有准循环特性。
2.2 π—旋转矩阵构造法
旋转矩阵构造法就是根据单位置换矩阵来构造校验矩阵的。它是由子矩阵构成校验矩阵，但是π—旋转矩阵构造法中的子矩阵为单位置换矩阵，其列重和行重都为1。校验矩阵是由多个子矩阵在横向和纵向排列得到的，所以具有更大的灵活性。子矩阵的大小的设计是要根据校验矩阵的列重、行重和码率、码长而决定的，并且子矩阵的大小对LDPC码性能有很大的影响。
2.3 准循环构造法
校验矩阵是由零矩阵和循环置换单位子矩阵构成的。有如下定义，循环置换子矩阵 Zi
是 z×z 阶单位阵循环移动 i 次得到的，其中，Z 是尺寸为 z×z 的零矩阵。则校验矩阵 H 为z×nz 阶，可构造如下：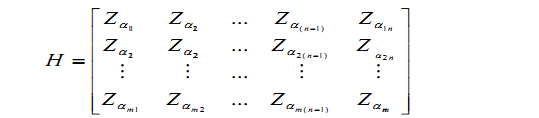

其中 α11 的取值范围是｛0,1，…，z-1，∞｝。
准循环LDPC码的存储量是原来的1/ Z，需要的存储量大幅度减少，是由于只需要存储循环置换单位子矩阵中第一行元素“1”的位置和准循环置换单位子矩阵在校验矩阵中的位置。准循环LDPC码是具有比较好的应用前景的，准循环结构的LDPC码是一种重要的LDPC码，已经被IEEE802.16e 标准和 GB20600 标准所采纳。
三、LDPC 码的编码算法
1、LU分解编码算法。LU分解法就是，首先对校验矩准循环LDPC码的存储量是原来的1/ Z，需要的存储量大幅度减少，是由于只需要存储循环置换单位子矩阵中第一行元素“1”的位置和准循环置换单位子矩阵在校验矩阵中的位置。准循环LDPC码是具有比较好的应用前景的，准循环结构的LDPC码是一种重要的LDPC码，已经被IEEE802.16e 标准和 GB20600 标准所采纳。
三、LDPC 码的编码算法
1、LU分解编码算法。LU分解法就是，首先对校验矩阵H的子矩阵H2 进行LU分解，可以得到上三角矩阵U和下三角矩阵L，然后再用前向迭代法就可以根据信息位来得到校验位，从而完成编码，LU分解编码算法运算的复杂度与码长 n 是成线性关系的。
2、部分迭代译码算法。LU分解法的缺点是预处理的复
杂度比较高，最重要的是经过预处理之后，新得到的校验矩阵有很大可能不是稀疏矩阵，所以会导致编码的运算量非常大。所以，我们想找到其他的编码算法，要求这种编码算法
的运算得复杂度和码长成线性关系。部分迭代译码算法就具有这样的特点，这种方法对校验矩阵H只做列置换和行置换，这样，矩阵的右上角会出现下三角形式，然后对矩阵进行分
块处理，把上述的下三角矩阵独立出来，使其成为一个子矩阵，最后根据这个子矩阵的结构来进行迭代编码。
四、LDPC 码的译码
1、消息传递算法。在消息传递算法中，其中概率信息是根据两部图在校验节点和变量节点之间的传递，逐步进行迭代译码。节点的沿边所发送的信息与上次接收到的信息是没有关系的，而是取决于与其相连的其他边上所接收到的信息。就是为了使任意一条边上，只有外来信息的传递，这样可以保证其译码性能的良好性。2、置信传播算法。置信传播算法就是，当消息传递算法中的译码过程中所发送的信息的符号集和信道所输出的符号集相同时，也就是采用连续性的消息时，适当选择信息映射函数。这种算法主要就是，根
据接收到的软信息在变量节点和校验节点之间进行迭代运算，来获得最大编码增益，因此具有良好的性能，在性能要求比较高的场合是适用的。3、最小和译码算法。最小和译码算法是根据对数域BP译码算法所提出的一种简化算法，最小和译码算法根据求最小值的运算从而简化了函数运算，不再需要估计信道噪声，而且运算复杂度也很大程度上降低了，但是它的性能也是有所下降的。4、BP迭代译码算法。基于BP算法的迭代译码算法，就是在给定接收信号和信道估计的条件下，在迭代的每一步中，对于有噪序列的每一个符号，都要进行后验概率的估计，然后把所估计到的值输入下一次迭代，这样可以获得更好的结果。
五、总结
LDPC码是一种接近香农极限的码，其校验矩阵是稀疏矩阵，译码具有线性复杂度。BP译码算法的错误是可以检测的；MS算法虽然降低了函数的复杂度,但是性能也是下降的；BF算法复杂度低、硬件实现简单,不需要复杂的计算，操作方便。但性能较BP算法有一定程度的降低,适用于对译码性能不高的场合。